Basics of NMR

Navigation menu

NMR principles

Very simply, a nucleus can be modeled as a positively charged spinning sphere. This rotation leads to a small magnetic field which is characterized by a magnetic moment: μ.

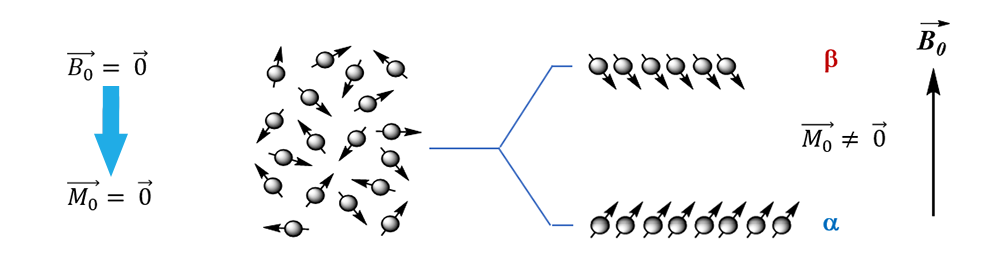
In a solution, the orientation of the magnetic moments of the nuclei is totally random and depends on the thermal agitation of the sample.

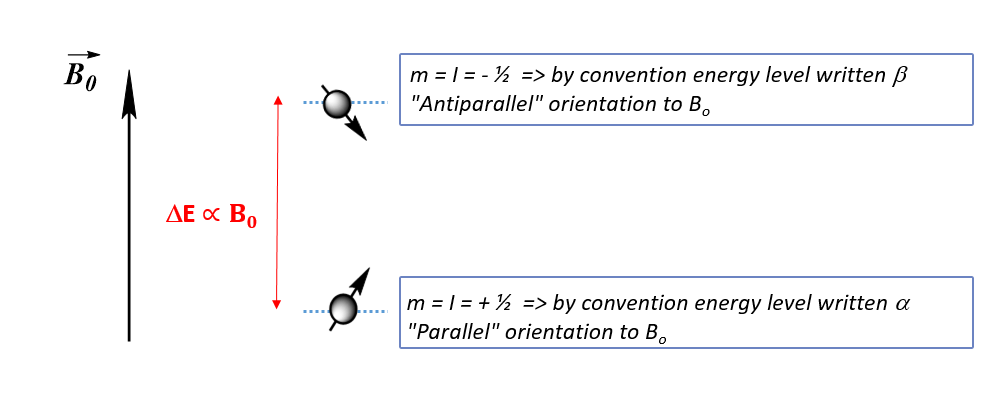
On the other hand, under the influence of an intense magnetic field B0 (of several Teslas) the nuclei are oriented according to the direction of the field. It is the spin number I that describes the behavior of magnetic moments under the action of this magnetic field, in particular the number of possible orientations of magnetic moments. Thus a nucleus with a spin number I = ½ can take two directions when it is subjected to a field B0: m = I = + ½ and m = I – 1 = - ½ = - I (with m: the magnetic quantum number).
The lowest energy state (m = - I) is generally written α, and the highest energy state β for a spin I = ½ .

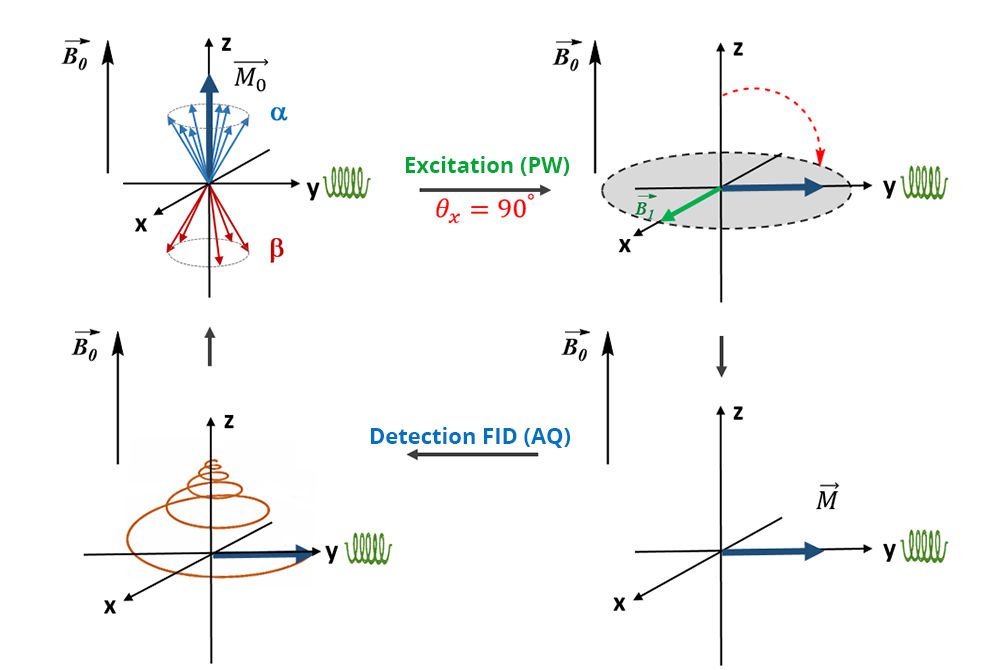
The nuclei (μ)subjected to a magnetic field B0 are oriented according to the direction of B0 along the longitudinal axis (z-axis). At equilibrium, the population of nuclei on the lowest energy level (α) is larger than that on the highest energy level (β). The sum of all magnetic moments leads to a macroscopic nuclear magnetization M, non-zero, parallel and following the same direction as the field along the z-axis. In addition, the magnetic moments μ are animated by a precession movement, around B0 => Larmor’s precession.
The precession movement occurs at the frequency 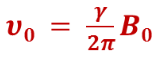V0 = gamma / 2 pi * B0(Larmor’s equation, with γ the gyromagnetic ratio of the nucleus considered).
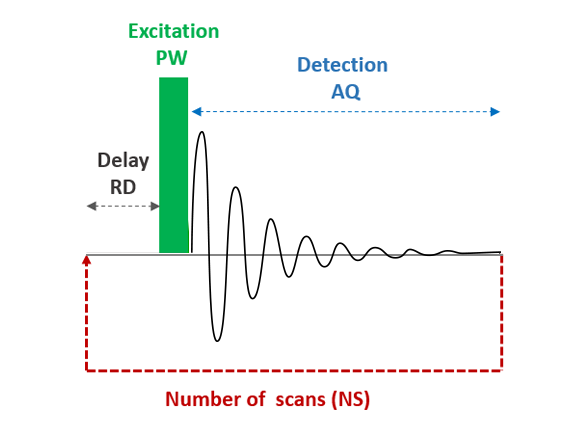
The NMR signal, which corresponds to the evolution over time of the nuclear magnetization after excitation, is induced in the transverse plane (detection coil). Therefore, at equilibrium the NMR signal detected is equal to zero.

Signal acquisition => excitation period and detection period
Diagram showing the phases of excitation (PW) and FID detection (AQ).
In the representation of the vector model, the application of a magnetic field B1 perpendicular to B0 (along the x-axis, for example) and corresponding to a tilting angle of θx = 90° makes it possible to equalize the populations of the levels α and β along the z-axis. This makes the nuclear longitudinal magnetization M zero along the z-axis and maximum in the transverse plane (along the y-axis). The magnetization is therefore perpendicular to B0. For reasons of clarity and simplification, only nuclear magnetization M is represented after the pulse θx. In general, the detected magnetization equals M0 sin θx
After excitation, field B1 is no longer applied. The magnetization that has been tilted into the transverse plane will change back to its equilibrium state, parallel to B0. This is the phenomenon of relaxation due to the different interactions that each nucleus faces (chemical shifts and couplings). The NMR data are recorded during this step. Two independent components are involved in the relaxation phenomenon: the longitudinal relaxation (T1) which accounts for the evolution of the magnetization along the longitudinal z-axis, and the cross-sectional relaxation (T2) which accounts for the evolution of the magnetization in the transverse plane.
Click on “Excitation” or “Detection FID” for explanations.

Once the magnetization M has returned to its equilibrium state along the z-axis, the excitation and detection sequence can be performed again to increase the signal-to-noise ratio on the spectrum ⇒ NS accumulations of the signal. The signal-to-noise ratio increases as a function of √NS

Next page
Previous page