Metrology

Each measure is accompanied by uncertainty. The measurement uncertainty characterizes the range of values within which the true value is supposed to lie with a certain degree of confidence.

Numerous factors can contribute to measurement uncertainty. When developing and validating a method, the influence of each of these factors must be assessed, and the associated uncertainties must be minimized.

The measurement uncertainty itself (related to the measurement method and the way it is implemented) must be distinguished from the uncertainty related to the sample variability (related to the sampling process), which is often considered separately.

Most of the time the uncertainty (called U) is expressed as a standard deviation. Expanded (or overall) uncertainty is defined as a multiple of this standard deviation. In practice, the recommended multiplication factor (>1, called the coverage factor) is equal to 2, i.e. the expanded uncertainty is equal to 2U (corresponding to a 95% confidence level that the true value is within this confidence interval).

The measurement result Z is then expressed as Z +/- U (see figure)

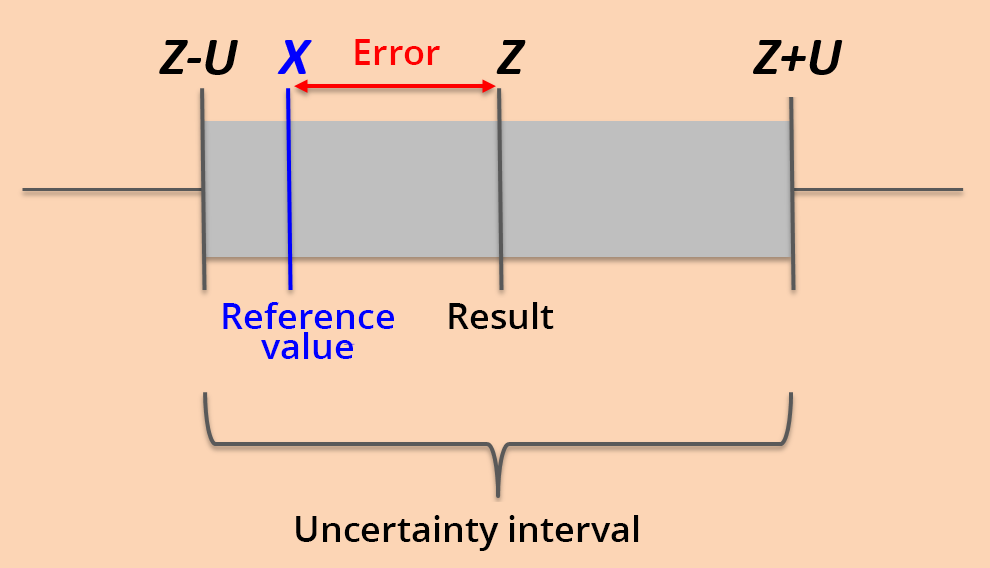
It is crucial to provide a measurement result with its uncertainty, in order to give an idea of the quality of the result and its reliability. If the measurement uncertainty is not provided, it will be very difficult to discuss and interpret the analytical result. Indeed, the measurement result is only an estimate of the measurand value – that is why an expression of the uncertainty of this estimate must be provided with this value.