Chimactiv - Interactive numerical educational resources for the analysis of complex media

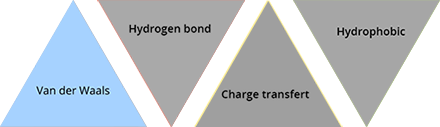
Van der Waals interactions

There are 3 types of Van der Waals forces:

Orientation forces (or Keesom forces)
Induction forces (or Debye forces)
Dispersion forces (or London forces)

Orientation forces

This interaction takes place between two polar molecules. Thus, a polar solvent (permanent dipole moment µ₁) will interact with a polar solute (dipole moment µ₂): the solute molecule tends to orient itself so that the two dipole moments are aligned.

The dipole-dipole energy of attraction is given by the relation:

$\large \large E = - \frac{2 \mu {_{1}}{^{2}} \cdot \mu {_{2}}{^{2}}} {3(4 \pi \varepsilon {_{0}}){^{2}} \cdot r{^{6}} \cdot k \cdot T }$

ε₀: permittivity of the medium
r: distance between the 2 dipoles
T: temperature

This energy is of the order of 25 to 40 kJ/mol.

Induction forces

This interaction takes place between a polar molecule and a polarizable molecule. Thus, a polar solvent (permanent dipole moment µ₁) will interact with a polarizable solute (polarizability α): the solute molecule acquires a dipole moment (µ_induced = α.E) under the effect of the electric field E created by the polar molecule, and orients itself so that the two dipole moments are aligned.

The dipole-dipole energy of attraction is given by the relation:

$\large E = - \frac{2 \alpha \cdot \mu {_{1}}{^{2}} } {4 \pi \varepsilon {_{0}} \cdot r{^{6}} }$

This energy is of the order of 8 to 25 kJ/mol.

Dispersion forces

Electrons are in continuous motion; atoms or molecules without a dipole therefore have, at any instant, a dipole moment resulting from the permanent deformation of their electronic cloud. This dipole moment acts on the electronic system of the neighboring molecule as a fluctuating polarizing dipole. This results in a mutual attraction, of the same kind as the permanent dipole-induced dipole interaction.

This energy is of the order of 5 to 20 kJ/mol.